Deus o Matemático Perfeito! A Proporção Áurea e a Sequência de Fibonacci Mostram Claramente Isto!

A Proporção Áurea e a Sequência De Fibonacci Estão em Nossos Corpos e em Tudo ao Nosso Redor

São os Padrões Matemáticos que Moldam Nosso Mundo e todo o Universo

Prof. Aécio D’Silva, Ph.D. e Equipe
AquaUniversity

Explore o fascinante mundo da proporção áurea e da sequência de Fibonacci, onde a matemática encontra a arte da natureza.

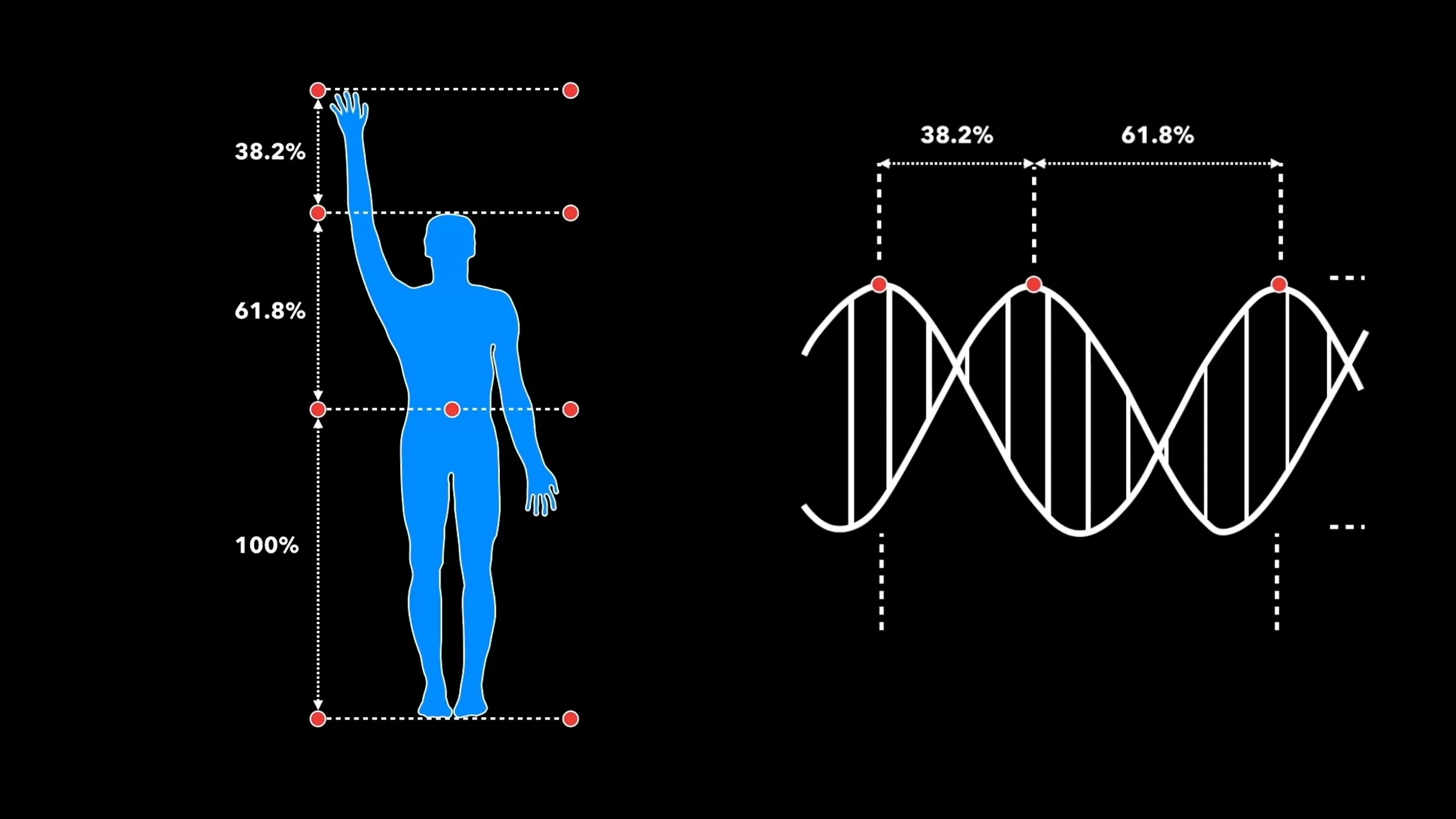
A Proporção Áurea e a Sequência De Fibonacci – A matemática é frequentemente vista como uma coleção de números e equações confinadas aos livros didáticos, mas a sua verdadeira beleza reside na sua prevalência no mundo que nos rodeia. Dois conceitos matemáticos que exemplificam isso são a proporção áurea e a sequência de Fibonacci – padrões que aparecem nos lugares mais inesperados, desde os DNA, as abelhas, as pétalas de uma flor até as espirais das galáxias.

A matemática é frequentemente vista como uma coleção de números e equações confinadas aos livros didáticos, mas a sua verdadeira beleza reside na sua prevalência no mundo que nos rodeia. Dois conceitos matemáticos que exemplificam isso são a proporção áurea e a sequência de Fibonacci – padrões que aparecem nos lugares mais inesperados, desde nos DNA, as pétalas de uma flor até as espirais das galáxias elas estão presentes.

Como veremos mais detalhado adiante, na sequência de Fibonacci, cada número é simplesmente a soma dos dois números anteriores (1, 1, 2, 3, 5, 8, 13, 21, 34, … etc.). No entanto, a sequência em si não é o aspecto mais crucial. O que importa é que, à medida que os números aumentam, a razão entre cada par sucessivo de números de Fibonacci se aproxima de 1,618, ou seu inverso, 0,618. Essa proporção é conhecida por vários nomes: proporção áurea, média áurea, ?, proporção divina, entre outros.

Então, por que esse número é tão significativo? Bem, muitos fenômenos naturais exibem propriedades dimensionais que aderem à razão de 1,618, sugerindo que desempenha um papel fundamental no tecido da natureza. Céptico? Considere as abelhas melíferas, por exemplo. Se você dividir o número de abelhas fêmeas pelo número de abelhas machos em uma determinada colmeia, você chegará a um número próximo a 1,618. No caso do DNA, se dividirmos seu comprimento pela sua largura (34 angstroms / 21 angstroms), chegaremos novamente a um número próximo de 1,618.  Os girassóis, com suas espirais opostas de sementes, demonstram uma razão de 1,618 entre os diâmetros de cada rotação. Essa proporção se manifesta em várias relações entre diferentes componentes ao longo da natureza.

Além disso, a proporção áurea encontra seu caminho nas artes devido ao seu apelo estético em comparação com outras proporções. Estruturas como o Partenon em Atenas, a Grande Pirâmide em Gizé e a Mona Lisa de Da Vinci incorporam retângulos cujas dimensões são baseadas na proporção áurea. Parece ser um aspecto inerente ao design e à composição.

O que são a Proporção Áurea e a Sequência de Fibonacci?

A Sequência de Fibonacci:

A Sequência de Fibonacci (SF) é infinita, onde os números seguintes são sempre a soma dos dois números anteriores. Ou seja, SF é uma série de números onde cada número é a soma dos dois anteriores, geralmente começando com 0 e 1.

Ou seja:

(0 +1), = 1,

(1 + 1) = 2,

(2 + 1) = 3,

(3 + 2) = 5,

(5 + 3) = 8,

(8 + 5) = 13,

(13 + 8) = 21,

(21 + 13) = 34,

(34 + 21) = 55,

(55 + 34) = 89,

 (89 + 55) = 144 …  e daí por diante.

A Proporção Áurea:

Por outro lado, a proporção áurea, também chamada de número de ouro, possui uma estreita relação com a sequência de Fibonacci. A proporção áurea é uma constante real algébrica irracional que representa, matematicamente, a “perfeição da natureza”.

A proporção áurea acontece quando um número maior da sequência de Fibonacci é dividido pelo número menor imediatamente anterior temos uma constante chamada de proporção áurea, denotada pela letra grega phi (?), é de aproximadamente 1,618.

3 /2 = 1.5

5/3 = 1.666

8/5 = 1.6

13/8 = 1.625

21/13 = 1.615

 34/21 = 1.619

 55/21 = 1.618

89/55 = 1.618

144/89 = 1.618

……………………

A Proporção Área ocorre também quando uma linha é dividida em duas partes de modo que a parte mais longa dividida pela parte mais curta ou igual a todo o comprimento dividido pela parte mais longa.

A Proporção Áurea na Natureza

A proporção áurea não é apenas uma curiosidade matemática; é um fenômeno natural. Isso pode ser visto no arranjo em espiral das folhas, no padrão das sementes de um girassol e na ramificação das árvores. Esta relação proporciona um sistema de ordem e equilíbrio, contribuindo para a eficiência e beleza das formas naturais num design inteligente.

A Sequência de Fibonacci (SF) é infinita, onde os números seguintes são sempre a soma dos dois números anteriores. Ou seja, SF é uma série de números onde cada número é a soma dos dois anteriores, geralmente começando com 0 e 1.

Ou seja:

(0 +1), = 1,

(1 + 1) = 2,

(2 + 1) = 3,

(3 + 2) = 5,

(5 + 3) = 8,

(8 + 5) = 13,

(13 + 8) = 21,

(21 + 13) = 34,

(34 + 21) = 55,

(55 + 34) = 89,

(89 + 55) = 144 …  e daí por diante.

Quem descobriu sequência de Fibonacci?

Muitas fontes afirmam que essa sequência foi descoberta ou “inventada” primeiramente por Leonardo Fibonacci. O matemático italiano, nascido por volta de 1170 d.C., era inicialmente conhecido como Leonardo de Pisa. No século XIX, historiadores criaram o apelido Fibonacci (significando aproximadamente “filho do clã Bonacci”) para distinguir o matemático de outro famoso Leonardo de Pisa.

Para chegar na sequência, Leonardo respondeu a seguinte questão: em condições ideais, quantos pares de coelhos poderiam ser produzidos a partir de um único par de coelhos num ano? Surpreendentemente, a resposta é 144 – e a fórmula usada para chegar a esta resposta não é outra senão a sequência de Fibonacci, 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,…. Este cenário hipotético pressupõe que as coelhas sempre dão à luz pares, constituídos por um macho e uma fêmea.

Veja como o cenário se desenrola: Inicialmente, dois coelhos recém-nascidos são colocados em um quintal cercado e deixados para procriar. No final do primeiro mês, resta apenas o par original, pois os coelhos não podem se reproduzir até completarem pelo menos um mês de idade. No final do segundo mês, o par original dá à luz, resultando em dois pares de coelhos. No terceiro mês, o casal original produz outro par de recém-nascidos enquanto a prole anterior atinge a maturidade, restando três pares de coelhos, dois dos quais se reproduzirão e darão mais dois pares no mês seguinte.

O número total de coelhos segue a sequência de Fibonacci. Após 12 meses, serão 144 pares de coelhos. Depois de dois anos, o número subiria para 46.368 pares!

A sequência de Fibonacci na natureza

Da mesma forma, a sequência de Fibonacci manifesta-se em vários aspectos da natureza. O número de pétalas de uma flor, o arranjo das brácteas de uma pinha e a forma como o falcão gira em espiral durante o vôo seguem essa sequência. É uma prova do papel da sequência nos padrões de crescimento dos organismos vivos.

Como Encontrar a Proporção Áurea

Encontrar a proporção áurea envolve um cálculo simples. Se você tiver um segmento de comprimento ‘a+b’, onde ‘a’ é a parte mais longa e ‘b’ é a parte mais curta, a proporção ‘a/b’ deve ser aproximadamente igual a 1,618, a proporção áurea.

Detectando a sequência de Fibonacci

Para identificar a sequência de Fibonacci, procure padrões que envolvam a soma dos dois números anteriores. Por exemplo, o número de espirais em uma pinha ou abacaxi normalmente segue a sequência.

A Proporção Áurea na Vida Diária

A proporção áurea é mais do que uma maravilha natural; é um princípio de design inteligente. Arquitetos e artistas o utilizaram para criar obras esteticamente agradáveis e harmoniosas. Também é usado em design de produtos, fotografia e até no mercado de ações para prever movimentos de preços.

A sequência de Fibonacci em nossas rotinas

A sequência de Fibonacci também tem aplicações práticas. É usado em algoritmos de computador, modelos financeiros e até mesmo em composição musical. O reconhecimento desta sequência pode fornecer insights sobre vários campos e fenômenos.

Como os cientistas usam a sequência de Fibonacci para estudar o crescimento das plantas?

Os cientistas usam a sequência de Fibonacci para estudar o crescimento das plantas, examinando os padrões em que as folhas, sementes e outras partes das plantas estão dispostas. Esses padrões geralmente seguem a sequência de Fibonacci, que pode ser vista no arranjo das folhas ao redor de um caule ou nas sementes na cabeça de um girassol. A sequência ajuda a otimizar a exposição da planta à luz solar e aos nutrientes, contribuindo para um crescimento eficiente.

O hormônio do crescimento nas plantas, a auxina e as proteínas que a transportam desempenham um papel crucial na criação desses padrões. A auxina influencia onde novas sementes ou folhas se formarão, e sua distribuição pode fazer com que a sequência de Fibonacci se manifeste no crescimento da planta. Por exemplo, simulações mostraram que a disposição das sementes de girassol em espirais, que seguem a sequência de Fibonacci, resulta da distribuição da auxina no meristema da planta.

Além disso, algumas plantas expressam a sequência de Fibonacci em seus pontos de crescimento, os locais onde os ramos se formam ou se dividem. Este padrão de crescimento permite o empacotamento mais eficiente de folhas ou sementes, maximizando a capacidade da planta de capturar recursos.

A compreensão destes padrões ajuda botânicos e biólogos a decifrar os princípios subjacentes ao crescimento e desenvolvimento das plantas, levando a insights sobre como as plantas se adaptam ao seu ambiente e como podem ser cultivadas para obter características desejáveis.

Sequência de Fibonacci na Genética

A sequência de Fibonacci está presente em muitos aspectos da genética, incluindo a estrutura do corpo humano e a molécula de DNA. A sequência de Fibonacci é composta por números que são a soma dos dois números anteriores. A sequência começa em 0 e 1, e a proporção de 34 angstroms para 21 angstroms na espiral de dupla hélice da molécula de DNA está próxima da proporção de Fibonacci de 1,6190476 para 1,6180339.

O modelo de dupla hélice do DNA baseia-se em duas suposições. Primeiro, a segunda regra de paridade de *Chargaff deve ser válida e, segundo, as frequências dos nucleotídeos devem aproximar-se dos valores limites quando o número de bases for suficientemente grande. Sob essas duas hipóteses, é possível prever com precisão as frequências dos nucleotídeos humanos.

*(Erwin Chargaff, professor de bioquímica na Faculdade de Medicina da Universidade de Columbia, fez contribuições significativas para a descoberta da estrutura de dupla hélice do DNA ao descobrir duas regras fundamentais durante sua carreira.)

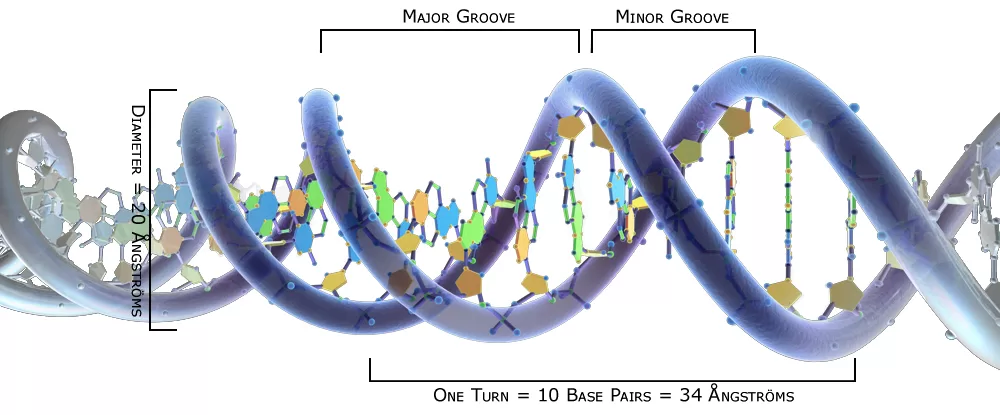
Este resultado pode ser usado como evidência para o modelo de cordas de Fibonacci que foi proposto para o crescimento de sequências repetitivas de DNA. Vale ressaltar que os valores previstos são soluções de um problema de otimização, comum em muitos fenômenos da natureza.

A sequência de Fibonacci também é usada para prever frequências de nucleotídeos humanos. O modelo assume que a segunda regra de paridade de Chargaff é válida e que as frequências dos nucleotídeos se aproximam dos valores limites quando o número de bases é grande o suficiente.

Sequência de Fibonacci e Moléculas de DNA. Como vimos antes, mesmo o reino microscópico não está imune a Fibonacci. A molécula de DNA mede 34 angstroms de comprimento por 21 angstroms de largura para cada ciclo completo de sua espiral de dupla hélice. Esses números, 34 e 21, são números da série Fibonacci, e sua proporção 1,6190476 se aproxima muito de Phi, 1,6180339.

Além disso, a cóclea da orelha e a espiral do cordão umbilical são espirais de Fibonacci. Diz-se que o rosto humano tem proporções iguais à proporção de Fibonacci, incluindo a relação entre olhos, ouvidos, boca e nariz.

Aqui estão algumas outras aplicações da sequência de Fibonacci na ciência

A sequência de Fibonacci tem uma ampla gama de aplicações em diversos campos científicos além de sua conhecida presença na natureza:

• Ciência da Computação : É usado em algoritmos para busca e classificação eficientes, como a técnica de busca de Fibonacci, e em estruturas de dados de Fibonacci (estrutura de dados baseada em árvore), que otimizam certas operações em programas de computador.
• Criptografia: A sequência contribui para o desenvolvimento de algoritmos criptográficos que garantem uma comunicação segura ao criar códigos complexos e difíceis de decifrar sem chave.
• Computação Quântica: Na computação quântica, a sequência de Fibonacci pode ser usada para modelar sistemas quânticos e compreender seu comportamento.
  

  

• Biologia: Além do crescimento das plantas, ajuda a modelar o crescimento populacional das espécies em condições ideais e pode ser visto na estrutura do DNA (como foi visto acima em Sequência de Fibonacci em Genética), e nos padrões de ramificação dos chifres ou conchas de alguns animais.
• Inteligência Artificial: A sequência auxilia na criação de algoritmos que podem aprender com os dados de uma maneira mais humana, aprimorando o aprendizado de máquina e as capacidades de inteligência artificial.

Essas aplicações demonstram a versatilidade da sequência de Fibonacci e seu profundo impacto no avanço do conhecimento científico e da tecnologia.

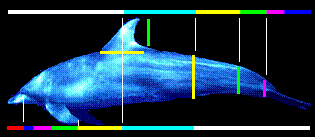
Como alguns peixes e espécies aquáticas expressam a sequência de Fibonacci em seus corpos e pontos de crescimento

No mundo aquático, a sequência de Fibonacci é expressa de diversas formas, refletindo a eficiência e otimização que este padrão matemático oferece na natureza. Aqui estão alguns exemplos de como peixes e espécies aquáticas exibem a sequência de Fibonacci:

• Filotaxia em Plantas Aquáticas: Algumas plantas aquáticas apresentam a sequência de Fibonacci na disposição de suas folhas ou pétalas, otimizando a exposição solar e a absorção de nutrientes.
• Conchas e Espirais: Muitas conchas, incluindo as de caracóis e náutilos, crescem num padrão espiral que pode ser descrito matematicamente pela sequência de Fibonacci. Isto permite um padrão de crescimento uniforme que é estruturalmente sólido e pode acomodar o tamanho crescente do organismo sem alterar a forma.
• Escamas de Peixe: O padrão das escamas em alguns peixes pode seguir a sequência de Fibonacci, o que pode estar relacionado à forma como as escamas crescem e fornecem proteção sem prejudicar a flexibilidade.
• Dentes e Espinhos: A disposição dos dentes em alguns animais aquáticos, ou os espinhos nas costas de um cavalo-marinho ou ouriço-do-mar, também podem apresentar padrões que se alinham com a sequência de Fibonacci, contribuindo para a sua eficácia funcional na defesa ou na predação.

Estes padrões não são apenas esteticamente agradáveis, mas também servem a propósitos práticos, contribuindo para a sobrevivência e eficiência das espécies aquáticas. A sequência de Fibonacci nestas estruturas biológicas é uma prova da influência generalizada da matemática no mundo natural.

Para concluir, a proporção áurea e a sequência de Fibonacci estão em tudo ao nosso redor e são excelentes exemplos de como a matemática está profundamente entrelaçada na estrutura do universo.  Eles nos lembram que existem as mãos de Deus, no projeto inteligente da vida, mostrando um padrão na criação da natureza. Ao compreender estes conceitos, podemos apreciar a majestade de Deus e encontrar inspiração no SEU design inteligente. Como disse Galileu: “Deus é de fato um matemático.”

Referências:

• A intrincada relação entre a proporção áurea e a sequência de Fibonacci na natureza https://www.treehugger.com/how-golden-ratio-manifests-nature-4869736
• https://www.mathnasium.com/blog/14-interesting-examples- da proporção áurea na natureza.
• Aplicações práticas da proporção áurea em arquitetura e design https://www.invisionapp.com/inside-design/golden-ratio-designers/
• https://www.adobe.com/creativecloud/design/discover/golden-ratio. HTML.
• O papel da sequência de Fibonacci nos mercados financeiros e algoritmos de computador https://numberdyslexia.com/fibonacci-sequence-real-life-examples/https://sage-answer.com/how-is-fibonacci-used-in-everyday- vida/.
• https://futurism.com/the-byte/fibonacci-quantum-computer.
• https://www.mathnasium.com/blog/14-interesting-examples-of-the-golden-ratio-in-nature